Get Full Text in PDF

Abstract

Visuals are the fundamental means to understand patterns, relationships and structure. The capacity for abstraction and generalisation of ideas is easily gained by visual learning. Mathematics must be taught in school by visual learning strategies to help students understand the concepts, develop problem solving skills and perceive real-world application. Visual representations are not only engaging, but they transform abstract mathematical concepts into physical tangible objects. Students need to learn using concrete objects and then progress to drawing models and pictorial representations. And as the last step, symbols and numbers must be used to write the idea in mathematical language. Conceptual knowledge is acquired as students progress from Concrete, to Pictorial, to Abstract ideas. Visual learning style kindles the innate curiosity in the child and motivates them to develop interest and passion for the subject. Focusing merely on memorization of facts and procedures does not result in deeper understanding of the mathematical skills and concepts. Conceptual understanding can be built by working on real-world problems, so the students can interpret, analyze and apply concepts. The classroom environment must give freedom to explore and encourage all students to participate and feel validated for their thinking. If Maths is taught as a natural, intuitive language that helps kids to express and communicate their thought process, then they can admire the subject for its aesthetic pleasure and practical utility.

The wonders in nature are described and illustrated in poetry, music and various art forms like paintings, photography and dance. Beauty in nature manifests as symmetry, rhythm and balance. These are the basic attributes of mathematics. Leonardo da Vinci understood that nature writes her laws in mathematical language. He realized that maths was the key to turning observations into theories. He revealed the beauty of nature in his art, architecture and scientific inventions. He said, “There is no certainty in sciences where mathematics cannot be applied.” Maths is the architecture of the whole universe. It is the language of nature and has the vocabulary to make sense of the world around us. Our inability to perceive nature and communicate in terms of maths only signifies the flaw in our education system.

Hemachandra, an Indian linguist, discovered a mathematical sequence in Sanskrit poems observing the rhythm of the syllables. He formulated the sequence and gave a simple proof by relating the sequence to the long and short beats of tabla, a percussion instrument. The same mathematical sequence was discovered by Fibonacci, when he wondered about the growth of population of rabbits. This sequence appears everywhere in nature, in the arrangement of leaves, petals, shells and more. Curiosity and imagination stimulate mathematical thinking. We must provide a nurturing environment for kids to follow their natural curiosity. Curiosity is expressed in the form of questions. There is no such thing as wrong questions. No matter how silly or unrelated they may seem, questions can lead an open mind to new discoveries.

When kids gain an awareness of the world, they learn to think mathematically about the world around them. Maths should be taught as a natural, intuitive language that helps kids to express and communicate their thought process. But Maths is taught as a foreign language, where we memorize the sounds but do not understand the language. We do not understand the context of the mathematical symbols, their application and context in the real world.

A class of 30 students were posed a challenge—everyone must shake hands with every other classmate and find the total number of handshakes, without repetition. The kids tried to act out the problem, drew diagrams and figured that it was much easier to solve the problem in a small group, consisting of 3 kids. As they increased the number of kids in the group, they noted down the number of kids and handshakes. With enough samples, they looked for a pattern and generalized the answer for 30 students. This experiential understanding and reasoning would have been lost had the kids been taught the formula for combinatorics initially. The formula n(n-1)/2 and replacing n by 30 can give the answer in a minute, but it gives no knowledge to the student who will forget this formula quickly if he memorizes it.

The capacity to understand and perceive numbers at the level of sensations is termed as ‘Number Sense’. Number is an abstract idea. Number sense is a fundamental way to relate numbers concretely and visually, so it becomes real to the student. Visual learning is a key to gain intuitive understanding of numbers. Visual representations are not only engaging, but they transform abstract mathematical concepts into physical, tangible objects. Professors at Stanford Graduate School of Education, US have found that visual learning has led to 50% average improvement in test scores, and boosted students’ engagement, persistence and mindset.* Some of the world’s top mathematicians engage almost entirely with visual maths.

Singapore has consistently scored on top in the Programme for International Student Assessment (PISA), a worldwide study of school students’ scholarly performance in mathematics, science, and reading.† The Singapore Maths program uses visual learning and succeeds in mastery of mathematical skills. Problems are taught with physical objects in a concrete way and then kids are asked to represent the idea as a diagram. Only in the last step, the problem is taught using numbers and symbols. These strategies have helped the kids to learn faster and effectively apply them. There are better ways to retain the knowledge, apart from repetitions of facts till the kids lose interest.

For instance, when multiplication is taught in traditional methods, kids are forced to rote memorize the multiplication tables, repeat them for endless times and given timed tests to evaluate if they have understood the concept. Memorizing the symbols and numbers first and then asking them to apply the same idea in real life makes no sense to the child, as they appear to be in two different worlds. In the Singapore Maths Program, kids learn using concrete materials like blocks or beads. They may count several 11 blocks and see a recurring pattern in it. Then they draw diagrams or are given visuals to represent the idea that was learnt. Finally, the teacher uses symbols and numbers to show them how to write the idea in mathematical language.

In India, visual learning is emphasized in lower grades in primary school, but given up after the early stages of education, assuming that it is not needed for high school students to learn abstract math. Estimation, pattern and spatial recognition can be taught only using images and physical objects. We readily accept that comparing size or estimating distance between objects needs visual learning to get the ‘sense of scale’. Similarly, we must teach ‘number sense’ using visual aids and manipulatives, so kids can understand maths and have the capacity to communicate their ideas. Seeing numbers in different ways is the key to develop number sense and to build fluency in maths language.

Using this method, children learn maths facts and their context. They can intuitively apply the abstract maths concepts in their everyday life, and their education stays relevant to their world. This motivates them to pay attention to what is taught and think about the ideas, even after the class ends.

The tools for teaching this approach are the very same tools that are discarded after primary school—puzzles, blocks, lego, dice, rubik’s cube and activities like paper folding, tracing points, magic tricks and toothpick modeling. Manjul Bhargava won the Fields Medal, which is considered as mathematics’ equivalent of the Nobel Prize, by using the simplest rubik’s cube. He also offers a seminar on “The Mathematics of Magic Tricks” in Princeton University, and is celebrated as an extraordinary professor by his students. This validates the point that games and puzzles are mathematical tools that cannot be ignored as childish toys to learn middle and high school maths.

Visual learning and the freedom to explore will allow kids to understand mathematical concepts that are reserved for college and researchers. Non-euclidean geometry is child’s play if the kid is allowed to draw shapes on paper and a ball, and compare the results. They may formulate their own fractals and compute irregular shapes by conducting experiments and generalization. We must remove the stigma on visual learning methods and build the classroom environment that encourages all students to participate and feel validated for their thinking. There is more than one answer to a question and there are different ways to arrive at an answer. We must celebrate success and also appreciate the mistakes in the classroom, as mistakes are an integral part of learning. Teachers can make the thinking process conscious but should help the students identify the different types of mistakes. Some mistakes are made during Eureka moments, when a new idea pops up and it is expressed without thinking through various facts. Mistakes are bound to happen when a child tries to apply a known concept to a new setting. These are bold mistakes that have to be encouraged, and kids must be rewarded for taking the adventure into the unknown. They must also be able to distinguish such bold mistakes from sloppy mistakes that should be avoided.

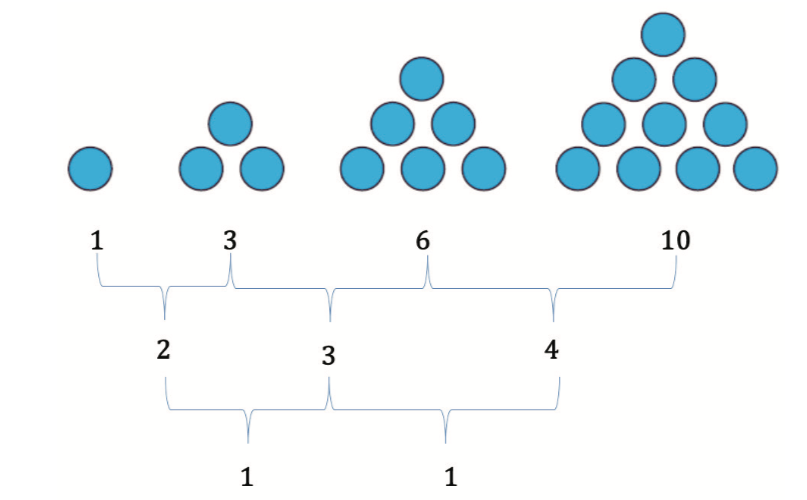
Calculus is taught as “the branch of maths that deals with limits and the differentiation and integration of functions of one or more variables”. If taught through visual learning methods, children can see the patterns and the way the patterns change in succession. This rate of change is the fundamental idea of calculus. Algebra formulates equations by finding patterns in numbers and calculus finds patterns in algebra.

Only few may be interested in getting into the details of calculus, but everyone should be able to admire maths and expand their minds in the process. We might not be interested in the acceleration of the rocket launched into space, but we are very much eager to know the rate of increase of our salary over time.

In the traditional method, teaching maths is to pose a question to kids and tell them the steps to find the answers. The focus is on memorizing the procedure to find the answer. Taught by this method, a child can apply the formula and solve a quadratic equation. But if a child is given the freedom to explore and guided to find patterns in them, he will find the infinite pattern that is hidden in the quadratic equation.

For example, to solve the equation, x2=2 the child is taught to plug in the values to the quadratic formula and solve for x.

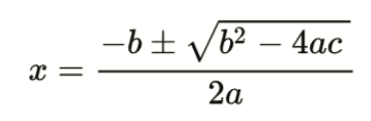
But if he is let to explore, he might discover the infinite-continued-fraction hidden in the equation.

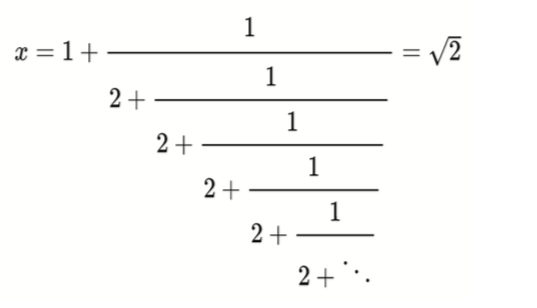
A high philosophical truth, “Infinity is contained in the finite”, can be realized by a child when he learns to think in the mathematical language. Learning without context makes maths a difficult and boring subject. When students gain fluency in maths concepts and mastery over the skills in an intuitive way, they can express their knowledge in any field of study.